


 中国权威高考信息资源门户 www.gaosao.com
中国权威高考信息资源门户 www.gaosao.com
概率与统计
考试内容:抽样方法.总体分布的估计.总体期望值和方差的估计.
考试要求:(1)了解随机抽样了解分层抽样的意义,会用它们对简单实际问题进行抽样.(2)会用样本频率分布估计总体分布.(3)会用样本估计总体期望值和方差.
概率与统计知识要点
一、随机变量.
1.随机试验的结构应该是不确定的.试验如果满足下述条件:
①试验可以在相同的情形下重复进行;②试验的所有可能结果是明确可知的,并且不止一个;③每次试验总是恰好出现这些结果中的一个,但在一次试验之前却不能肯定这次试验会出现哪一个结果.
它就被称为一个随机试验.
2.离散型随机变量:如果对于随机变量可能取的值,可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.若ξ是一个随机变量,a,b是常数.则
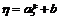 也是一个随机变量.一般地,若ξ是随机变量,
也是一个随机变量.一般地,若ξ是随机变量,
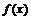 是连续函数或单调函数,则
是连续函数或单调函数,则
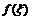 也是随机变量.也就是说,随机变量的某些函数也是随机变量.
也是随机变量.也就是说,随机变量的某些函数也是随机变量.
设离散型随机变量ξ可能取的值为:
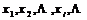
ξ取每一个值
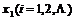 的概率
的概率
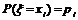 ,则表称为随机变量ξ的概率分布,简称ξ的分布列.
,则表称为随机变量ξ的概率分布,简称ξ的分布列.
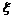
|
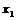
|
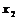
|
… |
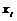
|
… |
| p |
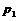
|
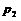
|
… |
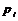
|
… |
有性质①
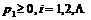 ; ②
; ②
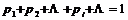 .
.
注意:若随机变量可以取某一区间内的一切值,这样的变量叫做连续型随机变量.例如:
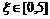 即
即
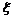 可以取0~5之间的一切数,包括整数、小数、无理数.
可以取0~5之间的一切数,包括整数、小数、无理数.
3.⑴二项分布:如果在一次试验中某事件发生的概率是p,那么在n次独立重复试验中这个事件恰好发生k次的概率是:
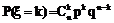 [其中
[其中
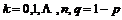 ]
]
于是得到随机变量ξ的概率分布如下:我们称这样的随机变量ξ服从二项分布,记作
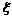 ~B(n·p),其中n,p为参数,并记
~B(n·p),其中n,p为参数,并记
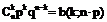 .
.
⑵二项分布的判断与应用.
①二项分布,实际是对n次独立重复试验.关键是看某一事件是否是进行n次独立重复,且每次试验只有两种结果,如果不满足此两条件,随机变量就不服从二项分布.
②当随机变量的总体很大且抽取的样本容量相对于总体来说又比较小,而每次抽取时又只有两种试验结果,此时可以把它看作独立重复试验,利用二项分布求其分布列.
4.几何分布:“
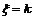 ”表示在第k次独立重复试验时,事件第一次发生,如果把k次试验时事件A发生记为
”表示在第k次独立重复试验时,事件第一次发生,如果把k次试验时事件A发生记为
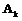 ,事A不发生记为
,事A不发生记为
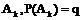 ,那么
,那么
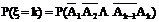 .根据相互独立事件的概率乘法分式:
.根据相互独立事件的概率乘法分式:
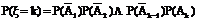
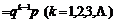 于是得到随机变量ξ的概率分布列.
于是得到随机变量ξ的概率分布列.
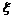
|
1 | 2 | 3 | … | k | … |
| p | q | qp |
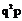
|
… |
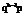
|
… |
我们称ξ服从几何分布,并记
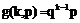 ,其中
,其中
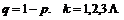
5.⑴超几何分布:一批产品共有N件,其中有M(M<N)件次品,今抽取
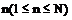 件,则其中的次品数ξ是一离散型随机变量,分布列为
件,则其中的次品数ξ是一离散型随机变量,分布列为
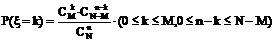 .〔分子是从M件次品中取k件,从N-M件正品中取n-k件的取法数,如果规定
.〔分子是从M件次品中取k件,从N-M件正品中取n-k件的取法数,如果规定
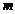 <
<
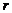 时
时
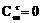 ,则k的范围可以写为k=0,1,…,n.〕
,则k的范围可以写为k=0,1,…,n.〕
⑵超几何分布的另一种形式:一批产品由a件次品、b件正品组成,今抽取n件(1≤n≤a+b),则次品数ξ的分布列为
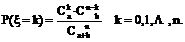 .
.
⑶超几何分布与二项分布的关系.
设一批产品由a件次品、b件正品组成,不放回抽取n件时,其中次品数ξ服从超几何分布.若放回式抽取,则其中次品数
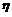 的分布列可如下求得:把
的分布列可如下求得:把
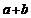 个产品编号,则抽取n次共有
个产品编号,则抽取n次共有
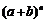 个可能结果,等可能:
个可能结果,等可能:
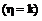 含
含
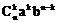 个结果,故
个结果,故
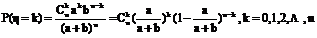 ,即
,即
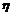 ~
~
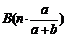 .[我们先为k个次品选定位置,共
.[我们先为k个次品选定位置,共
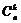 种选法;然后每个次品位置有a种选法,每个正品位置有b种选法]可以证明:当产品总数很大而抽取个数不多时,
种选法;然后每个次品位置有a种选法,每个正品位置有b种选法]可以证明:当产品总数很大而抽取个数不多时,
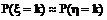 ,因此二项分布可作为超几何分布的近似,无放回抽样可近似看作放回抽样.
,因此二项分布可作为超几何分布的近似,无放回抽样可近似看作放回抽样.
二、数学期望与方差.
1.期望的含义:一般地,若离散型随机变量ξ的概率分布为
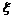
|
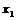
|
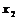
|
… |
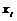
|
… |
| p |
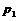
|
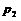
|
… |
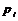
|
… |
则称
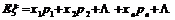 为ξ的数学期望或平均数、均值.数学期望又简称期望.数学期望反映了离散型随机变量取值的平均水平.
为ξ的数学期望或平均数、均值.数学期望又简称期望.数学期望反映了离散型随机变量取值的平均水平.
2.⑴随机变量
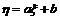 的数学期望:
的数学期望:
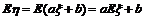
①当
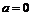 时,
时,
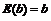 ,即常数的数学期望就是这个常数本身.
,即常数的数学期望就是这个常数本身.
②当
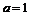 时,
时,
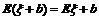 ,即随机变量ξ与常数之和的期望等于ξ的期望与这个常数的和.
,即随机变量ξ与常数之和的期望等于ξ的期望与这个常数的和.
③当
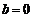 时,
时,
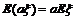 ,即常数与随机变量乘积的期望等于这个常数与随机变量期望的乘积.
,即常数与随机变量乘积的期望等于这个常数与随机变量期望的乘积.
| ξ | 0 | 1 |
| p | q | p |
⑵单点分布:
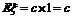 其分布列为:
其分布列为:
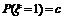 .
.
⑶两点分布:
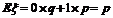 ,其分布列为:(p+q=1)
,其分布列为:(p+q=1)
⑷二项分布:
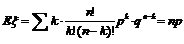 其分布列为
其分布列为
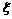 ~
~
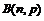 .(p为发生
.(p为发生
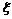 的概率)
的概率)
⑸几何分布:
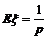 其分布列为
其分布列为
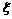 ~
~
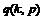 .(p为发生
.(p为发生
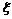 的概率)
的概率)
3.方差、标准差的定义:当已知随机变量ξ的分布列为
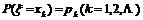 时,则称
时,则称
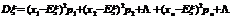 为ξ的方差.显然
为ξ的方差.显然
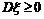 ,故
,故
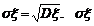 为ξ的根方差或标准差.随机变量ξ的方差与标准差都反映了随机变量ξ取值的稳定与波动,集中与离散的程度.
为ξ的根方差或标准差.随机变量ξ的方差与标准差都反映了随机变量ξ取值的稳定与波动,集中与离散的程度.
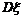 越小,稳定性越高,波动越小.
越小,稳定性越高,波动越小.
4.方差的性质.
⑴随机变量
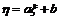 的方差
的方差
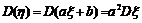 .(a、b均为常数)
.(a、b均为常数)
| ξ | 0 | 1 |
| p | q | p |
⑵单点分布:
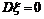 其分布列为
其分布列为
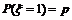
⑶两点分布:
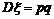 其分布列为:(p+q=1)
其分布列为:(p+q=1)
⑷二项分布:
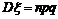
⑸几何分布:
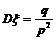
5.期望与方差的关系.
⑴如果
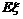 和
和
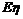 都存在,则
都存在,则
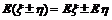
⑵设ξ和
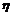 是互相独立的两个随机变量,则
是互相独立的两个随机变量,则
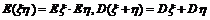
⑶期望与方差的转化:
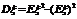 ⑷
⑷
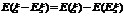 (因为
(因为
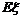 为一常数)
为一常数)
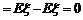 .
.
三、正态分布.(基本不列入考试范围)
1.密度曲线与密度函数:对于连续型随机变量ξ,位于x轴上方,ξ落在任一区间
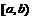 内的概率等于它与x轴.直线
内的概率等于它与x轴.直线
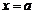 与直线
与直线
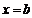 所围成的曲边梯形的面积
所围成的曲边梯形的面积
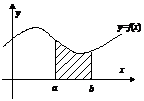 (如图阴影部分)的曲线叫ξ的密度曲线,以其作为
(如图阴影部分)的曲线叫ξ的密度曲线,以其作为
图像的函数
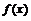 叫做ξ的密度函数,由于“
叫做ξ的密度函数,由于“
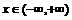 ”
”
是必然事件,故密度曲线与x轴所夹部分面积等于1.
2.⑴正态分布与正态曲线:如果随机变量ξ的概率密度为:
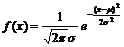 .(
.(
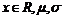 为常数,且
为常数,且
 ),称ξ服从参数为
),称ξ服从参数为
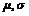 的正态分布,用
的正态分布,用
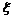 ~
~
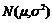 表示.
表示.
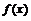 的表达式可简记为
的表达式可简记为
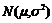 ,它的密度曲线简称为正态曲线.
,它的密度曲线简称为正态曲线.
⑵正态分布的期望与方差:若
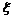 ~
~
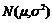 ,则ξ的期望与方差分别为:
,则ξ的期望与方差分别为:
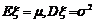 .
.
⑶正态曲线的性质.
①曲线在x轴上方,与x轴不相交.
②曲线关于直线
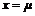 对称.
对称.
③当
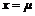 时曲线处于最高点,当x向左、向右远离时,曲线不断地降低,呈现出“中间高、两边低”的钟形曲线.
时曲线处于最高点,当x向左、向右远离时,曲线不断地降低,呈现出“中间高、两边低”的钟形曲线.
④当
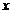 <
<
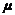 时,曲线上升;当
时,曲线上升;当
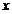 >
>
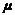 时,曲线下降,并且当曲线向左、向右两边无限延伸时,以x轴为渐近线,向x轴无限的靠近.
时,曲线下降,并且当曲线向左、向右两边无限延伸时,以x轴为渐近线,向x轴无限的靠近.
⑤当
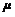 一定时,曲线的形状由
一定时,曲线的形状由
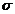 确定,
确定,
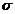 越大,曲线越“矮胖”.表示总体的分布越分散;
越大,曲线越“矮胖”.表示总体的分布越分散;
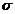 越小,曲线越“瘦高”,表示总体的分布越集中.
越小,曲线越“瘦高”,表示总体的分布越集中.
3.⑴标准正态分布:如果随机变量ξ的概率函数为
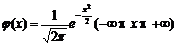 ,则称ξ服从标准正态分布.即
,则称ξ服从标准正态分布.即
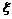 ~
~
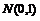 有
有
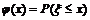 ,
,
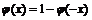 求出,而p(a<
求出,而p(a<
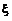 ≤b)的计算则是
≤b)的计算则是
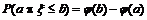 .
.
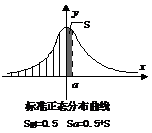 注意:当标准正态分布的
注意:当标准正态分布的
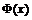 的X取0时,有
的X取0时,有
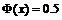 当
当
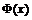 的X取大于0的数时,有
的X取大于0的数时,有
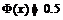 .比如
.比如
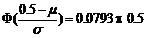 则
则
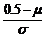 必然小于0,如图.
必然小于0,如图.
⑵正态分布与标准正态分布间的关系:若
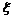 ~
~
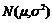 则ξ的分布函数通
则ξ的分布函数通
常用
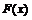 表示,且有
表示,且有
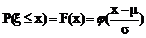 .
.
4.⑴“3
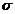 ”原则.
”原则.
假设检验是就正态总体而言的,进行假设检验可归结为如下三步:①提出统计假设,统计假设里的变量服从正态分布
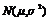 .②确定一次试验中的取值
.②确定一次试验中的取值
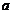 是否落入范围
是否落入范围
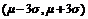 .③做出判断:如果
.③做出判断:如果
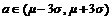 ,接受统计假设.如果
,接受统计假设.如果
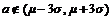 ,由于这是小概率事件,就拒绝统计假设.
,由于这是小概率事件,就拒绝统计假设.
⑵“3
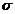 ”原则的应用:若随机变量ξ服从正态分布
”原则的应用:若随机变量ξ服从正态分布
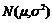 则ξ落在
则ξ落在
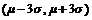 内的概率为99.7%亦即落在
内的概率为99.7%亦即落在
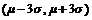 之外的概率为0.3%,此为小概率事件,如果此事件发生了,就说明此种产品不合格(即ξ不服从正态分布).
之外的概率为0.3%,此为小概率事件,如果此事件发生了,就说明此种产品不合格(即ξ不服从正态分布).
四、统计与统计案例



以上,就是30高考网小编给大家带来的2016年高考数学概率与统计题型怎么复习全部内容,希望对大家有所帮助!









